About

I am a 5th year applied mathematics Ph.D. student at the University of Minnesota. I am co-advised by Prof. Mitchell Luskin and Prof. Alexander Watson. I earned an Honors B.S. in applied mathematics and B.A. in physics at University of Chicago in 2021.

My research interest lies in the mathematical modeling, computation and numerical analysis with applications to condensed matter physics. I have been working on modeling the electronic properties of two-dimensional materials, especially twisted bilayer graphene (TBG). I greatly appreciate the support from UMN Doctoral Dissertation Fellowship.

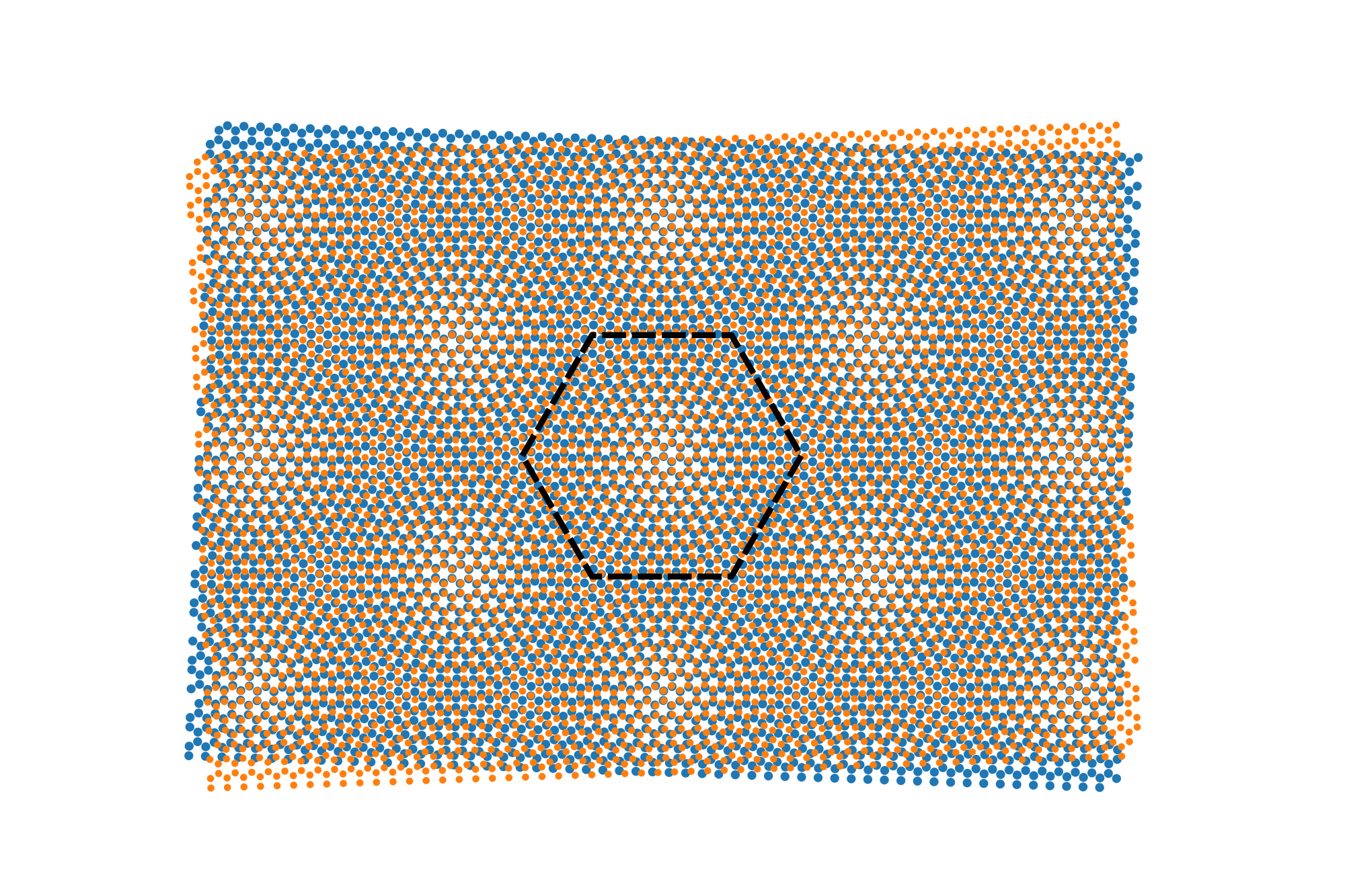Atomic structure of twisted bilayer graphene, with an approximate periodic pattern

Fall 2025: I am currently on the postdoc job market!