Research

Twisted bilayer graphene, created by stacking two graphene sheets with a slight twist, has garnered tremendous interest recently. The overarching goal of my work is to establish mathematical frameworks and computational methods for understanding novel quantum phenomena such as superconductivity that were realized in such materials.

Domain Truncation of Tight-binding model

The tight-binding model is a mathematical approach used to describe the movement of a single electron through the material. In this model, negatively charged electrons are considered “bound” to positively charged atomic sites, with a probability of “hopping” to neighboring atoms. This hopping probability decreases exponentially as the distance between atoms increases. The quantum dynamics of electrons is governed by the Schrödinger equation $i \partial_t \psi = H\psi,$ where the Hamiltonian $H$ records the hopping strength between atom sites, and the wave function $\psi$ is a discrete sequence related to the probability of finding the electron at a certain atom. The model is relatively simple yet it is powerful for predicting energy levels and conductivity in materials.

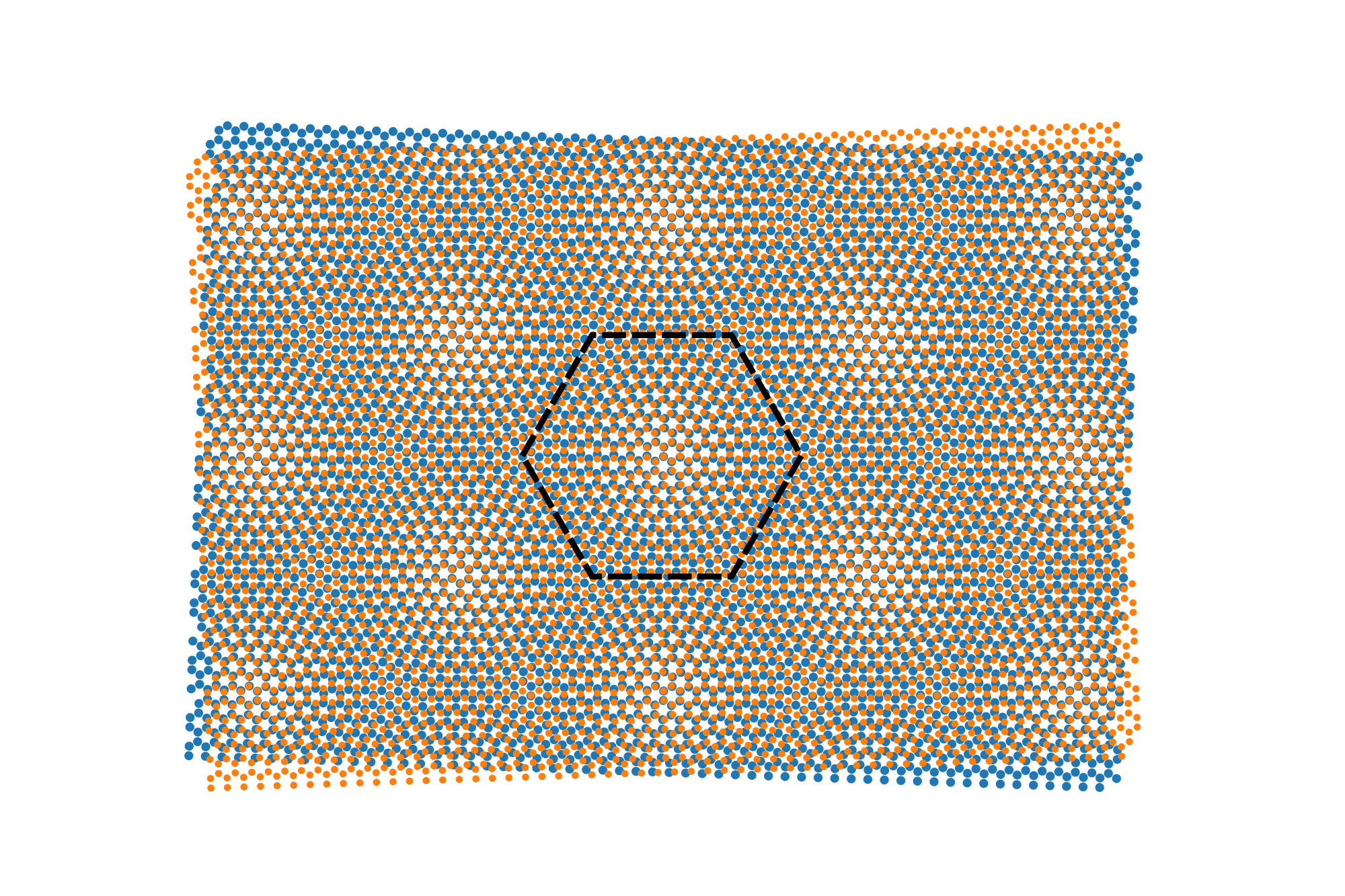Atomic structure of twisted bilayer graphene, with an approximate periodic pattern

Accurately solving the the Schrödinger equation is challenging by the fact that the model contains an infinite number of atoms, and is not periodic. In this paper, I developed a method to compute the time evolution of a single electron in the tight-binding model for TBG. The method relies on estimating the speed at which an electron can propagate through the material, given that the electron’s ability to “hop” between atoms decreases exponentially with distance. By considering only interactions within a finite radius $R$, I derived an error estimate that quantifies the difference between solutions of the truncated model $\psi_{\text{TB}, R}$ and the full infinite system $\psi_{\text{TB}}$ \(\|\psi_{\text{TB}}(t) - \psi_{\text{TB}, R}(t) \| \leq CR^{\frac{5}{2}}e^{-\kappa \left( v_{\max}(R - r) - t\right)}.\) This estimate ensures that computations on a finite domain are valid for a given range of time if $R$ is sufficiently large.

Effective Continuum Dynamics

Bistritzer and MacDonald observed that the single-particle electronic properties of TBG can often be captured by effective simplified models. The Bistritzer-MacDonald (BM) Hamiltonian is a system of partial differential equations that is periodic over the moiré pattern. This effective model correctly predicted essential features like flat electron energy bands near the “magic angle,” where superconductivity and other exotic phases emerge. 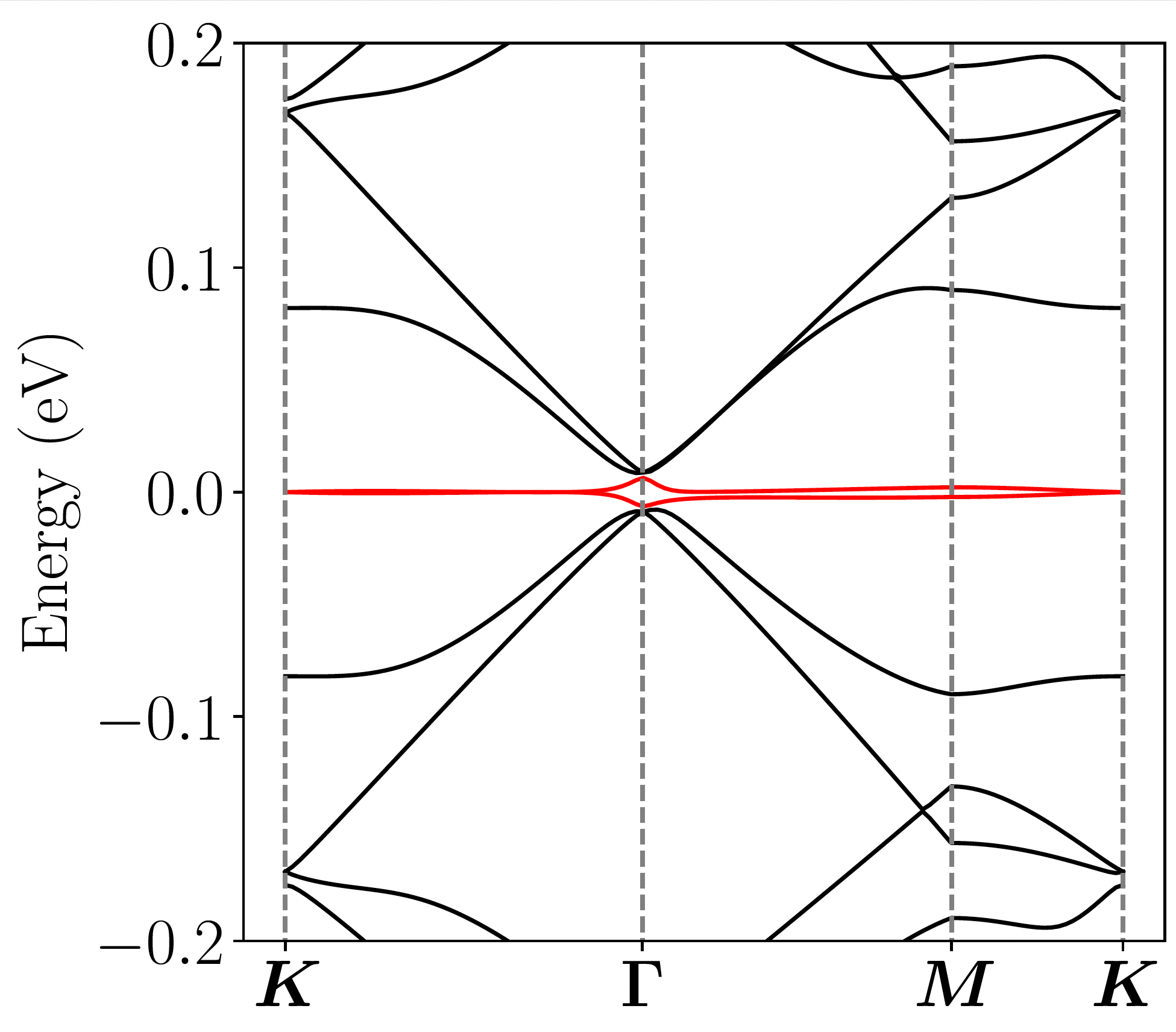BM band structure for TBG

The importance of this theoretical simplification motivates the question of the range of validity of such effective continuum models. In this paper, I used a multi-scale approach to study wave-packet solutions of the tight-binding model in TBG. The difference between the wave-packet time-evolved by the tight-binding model $\psi_{\text{TB}}(t)$, and that by the BM model $\psi_{\text{BM}}(t)$ is \(\| \psi_{\text{TB}}(t) - \psi_{\text{BM}}(t) \| \leq C \varepsilon^2 t,\) where $\varepsilon$ is the spectral width of the wave-packet.

To improve the BM model’s accuracy, I extended the multi-scale analysis to higher orders in my third paper. The main result yields a new effective model that reduces the error to \(\| \psi_{\text{TB}}(t) - \psi_{\text{BM, higher}}(t) \| \leq C \varepsilon^{3} t.\) I also carried out numerical simulations demonstrating that the higher-order model captures additional features absent in the original BM model. These findings suggest the higher-order accurate model captures important aspects of the physics of these materials.

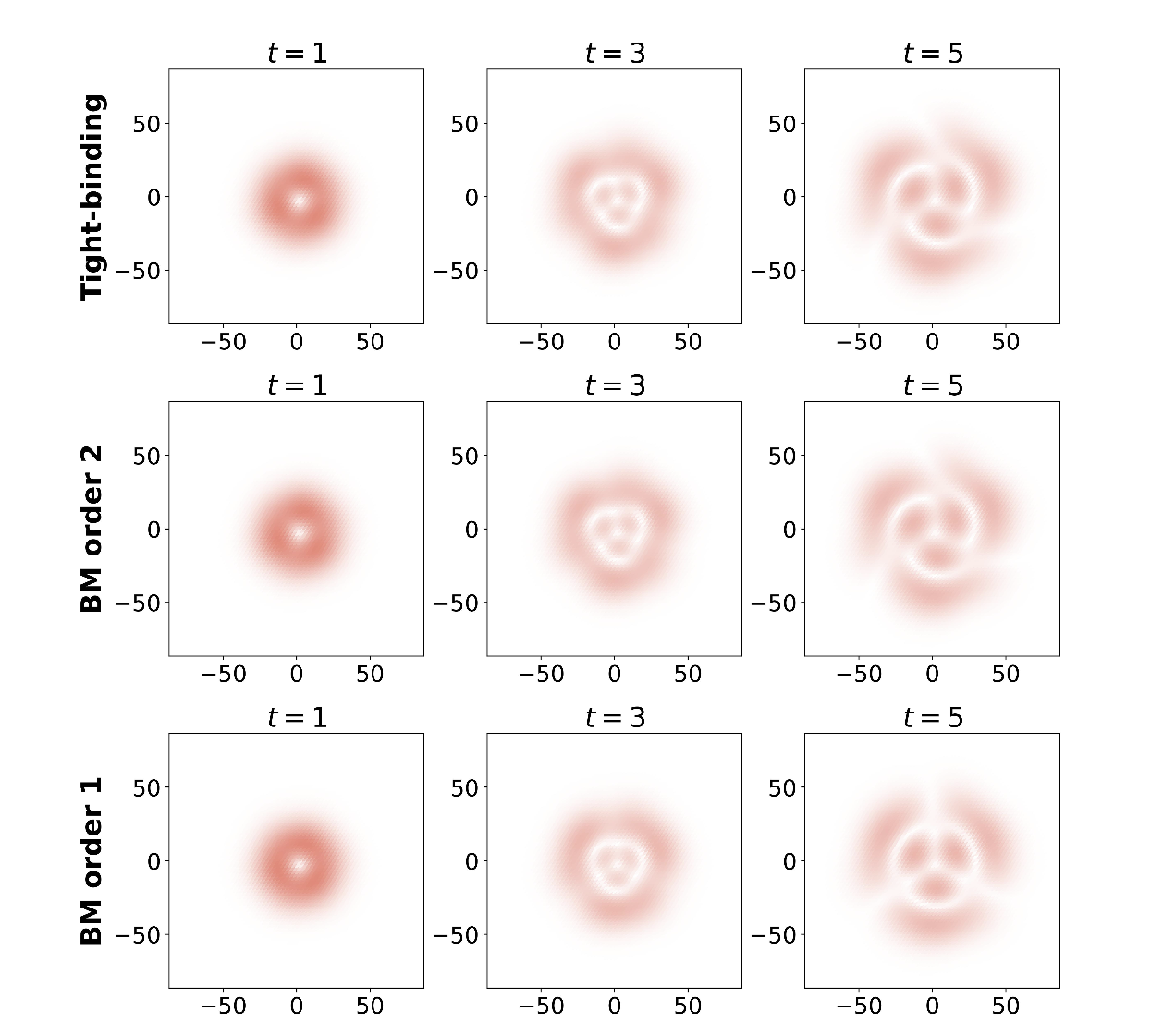Numerical simulations of wave packets

Electron interactions with relaxation

Much of the theoretical work on TBG has been based on analysis of the Bistritzer-MacDonald model which includes a phenomenological parameter to account for lattice relaxation. In this work, we use a newly developed continuum model which systematically accounts for the effects of structural relaxation. In particular, we model structural relaxation by coupling linear elasticity to a stacking energy that penalizes disregistry. We compare the impact of the two relaxation models on the corresponding many-body model by defining an interacting model projected to the flat bands.